I’m far from an epidemiologist, but odds ratios and relative risk come up often enough that it’s handy to have a solid understanding of what they mean. These measures are used when faced with contingency tables:

where 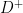 is having a disease/condition/event under study and
is having a disease/condition/event under study and 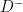 is not having the disease/condition/event under study. Also
is not having the disease/condition/event under study. Also  is testing positive/symptomatic/presence of a particular trait and
is testing positive/symptomatic/presence of a particular trait and  is testing negative/asymptomatic/not having a particular trait.
is testing negative/asymptomatic/not having a particular trait.
Odds ratio
The odds of success is the ratio of the probability of success 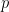 to the chance of failure
to the chance of failure 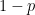 :
:
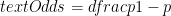 .
.
In the context of disease testing, we’d consider the odds of a disease for  people (those with particular traits) against the
people (those with particular traits) against the  group (people without a particular trait). The probability of having a disease for the
group (people without a particular trait). The probability of having a disease for the  group can be found by restricting attention to the
group can be found by restricting attention to the  row (restrict attention to the people who have the trait) and working out what proportion of those people have the disease:
row (restrict attention to the people who have the trait) and working out what proportion of those people have the disease:
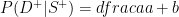
and the probability of having a disease for the  group is
group is
 .
.
Hence the odds of disease for  patients is:
patients is:

and the odds of disease for  people is:
people is:
 .
.
Finally the odds ratio is:
 .
.
That last step is just algebra.
What does it mean?
The odds ratio is a measure of effect size – how much of a difference does the positive test/symptoms/particular trait have on your chances of getting the disease? An odds ratio of 1 indicates that the disease/condition/event under study is equally likely to occur in both groups (that is to say 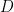 and
and  are independent of one another). An odds ratio greater than 1 indicates that the disease more likely to occur in the
are independent of one another). An odds ratio greater than 1 indicates that the disease more likely to occur in the  group than the
group than the  group. Similarly, an odds ratio less than 1 indicates that the disease is less likely to occur in the
group. Similarly, an odds ratio less than 1 indicates that the disease is less likely to occur in the  group.
group.
For example an odds ratio of 2 indicates that people from the  group had twice the risk of having the disease as people from the
group had twice the risk of having the disease as people from the  group.
group.
When can you use it?
The odds ratio can be used in observational studies (examining the effect of a risk factor/symptom on the disease outcome), prospective studies (where subjects who are initially identified as “disease-free” and classified by presence or absence of a risk factor are followed over time to see if they develop the disease) and retrospective studies (subjects are followed back in time to check for the presence or absence of the risk factor for each individual).
Relative risk
The relative risk is a measure of the influence of risk on disease. It is the probability of contracting the disease given you have the risk factor divided by the probability of contracting the disease given you don’t have the risk factor:
 .
.
What does it mean?
A relative risk of 1 means there is no difference in risk (of contracting the disease) between the two groups. A relative greater than 1 means the disease is more likely to occur in the  group than in the
group than in the  group. A relative risk less than 1 means the disease is more likely to occur in the
group. A relative risk less than 1 means the disease is more likely to occur in the  group than in the
group than in the  group.
group.
For example a relative risk of 2 would mean that  people would be twice as likely to contract the disease than people from the
people would be twice as likely to contract the disease than people from the  group.
group.
When can you use it?
Relative risk can only be used in prospective studies – note the wording above is all in terms of “contracting” the disease. It is often used to compare the risk of developing a disease in people not receiving a new medical treatment (or receiving a placebo) versus people who are receiving an established treatment.
Odds ratio vs relative risk
Odds ratios and relative risks are interpreted in much the same way and if  and
and  are much less than
are much less than 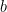 and
and  then the odds ratio will be almost the same as the relative risk. In some sense the relative risk is a more intuitive measure of effect size. Note that the choice is only for prospective studies were the distinction becomes important in cases of medium to high probabilities. If action A carries a risk of 99.9% and action B a risk of 99.0% then the relative risk is just over 1, while the odds associated with action A are more than 10 times higher than the odds with B.
then the odds ratio will be almost the same as the relative risk. In some sense the relative risk is a more intuitive measure of effect size. Note that the choice is only for prospective studies were the distinction becomes important in cases of medium to high probabilities. If action A carries a risk of 99.9% and action B a risk of 99.0% then the relative risk is just over 1, while the odds associated with action A are more than 10 times higher than the odds with B.
This not being my area, naturally I turned to Wikipedia, which suggests that the odds ratio is commonly used for case-control studies, as odds, but not probabilities, are usually estimated whereas relative risk is used in randomized controlled trials and cohort studies.
Finally (and the real motivation for the post), an award winning video has been made by Susanna Cramb discussing the differences between odds ratios and relative risk:
